Check out today’s Step 1 Qmax Question Challenge.
Know the answer? Post it below! Don’t forget to check back for an update with the correct answer and explanation (we’ll post it in the comments section below).
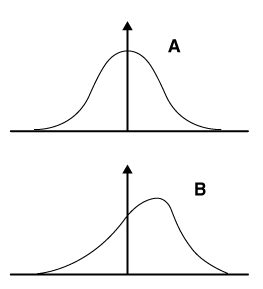The statistical distribution of two studies is shown below. The mean is equal to the median and the mode in the first curve (labeled A).
Which of the following correctly describes the mean, median, and mode in the second curve (labeled B)?
A. Mean < median < mode
B. Mean < mode < median
C. Median < mean < mode
D. Median < mode < mean
E. Mode < mean < median
F. Mode < median < mean
———————–
Want to know the ‘bottom line?’ Purchase a USMLE-Rx Subscription and get many more features, more questions, and passages from First Aid, including images, references, and other facts relevant to this question.
This practice question is an actual question from the USMLE-Rx Step 1 Qmax test bank. For more USMLE Step 1 prep, subscribe to our First Aid Step 1 Flash Facts and First Aid Step 1 Express Videos video series. Score the best deal on all three products as a bundle with USMLE-Rx 360 Step 1.
A, its a Negative Skewed graph, Tail on the Left, where Mean is the smallest and Mode has the highest value..a Median is always in the middle of the 2 …
A
A
A
The correct answer is A. The first curve, with mean = median = mode, represents a normal Gaussian distribution. The second curve represents a negative skew. The tail of the distribution is always in the direction of skew: in a negative skew, the area negative/left relative to the peak will be greater than that to the right. In a negatively skewed population (eg, a data set with the points 20, 39, 40, 41, and 41) the mean (36) is significantly lower than the median (40) which is less than the mode (41). The mode is equal to the most common result. This is represented at the top of the curve. The median is the middle value if the value were ordered sequentially. It turns out that during either a positive skew or a negative skew, the median is in between the mean and the mode. Therefore, mean < median < mode.
B is not correct. In Gaussian distributions, the median is always between the mode and the mean.
C is not correct. In Gaussian distributions, the median is always between the mode and the mean.
D is not correct. In Gaussian distributions, the median is always between the mode and the mean.
E is not correct. In Gaussian distributions, the median is always between the mode and the mean.
F is not correct. This would be the case in a positively skewed data distribution, rather than a negative skew.
Thank you for explanation .
It’s great to review this way!
Thank you!